Μία σελίδα για τα Μαθηματικά

Εφαρμογές του κύκλου στη Φυσική

Στο παραπάνω link δίνεται εφαρμογή σε geogebra που σχετίζεται με την παρουσίαση "Ο κύκλος και εφαρμογές του" https://ptsampouka.sites.sch.gr/index.html
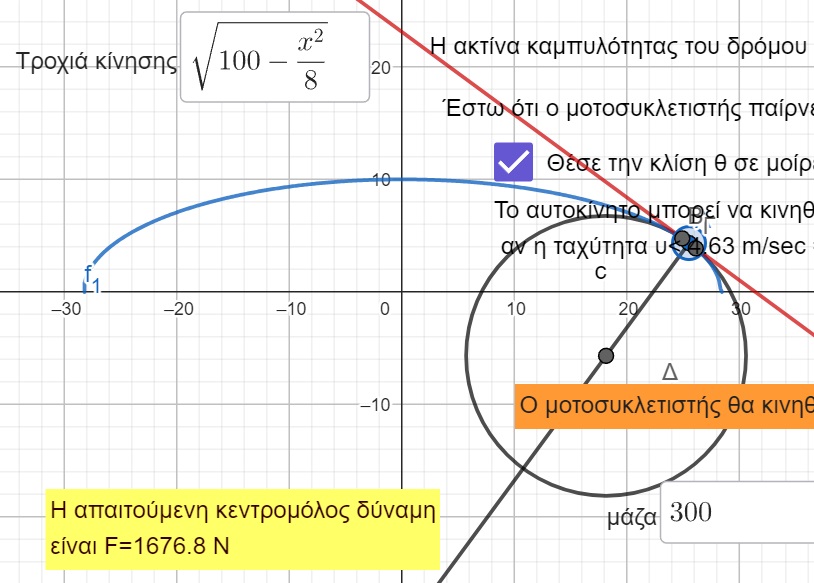
Η εφαρμογή υλοποιεί την προσέγγιση μιας καμπύλης που καθορίζεται βάσει μαθηματικού τύπου που εισάγει ο χρήστης από τόξο κύκλου που υπολογίζεται από 3 πολύ κοντινά σημεία που λαμβάνονται πάνω στην περιφέρεια του κύκλου. Από τον κύκλο, τόξο του οποίου προσεγγίζει τοπικά στοιχειώδες τμήμα της καμπύλης, προκύπτει η ακτίνα καμπυλότητας στο συγκεκριμένο σημείο της τροχιάς του οχήματος. Θεωρώντας μηδενική τριβή από το οδόστρωμα η κεντρομόλος δύναμη που απαιτείται για να διατηρήσει ένας μοτοσυκλετιστής την τρόχια του καθορίζεται αποκλειστικά από την κλίση του δρόμου και τη μάζα του οχήματος, στοιχεία τα μπορεί μπορεί να εισάγει σε ειδικά πεδία ο χρήστης της εφαρμογής ενώ η μέγιστη στιγμίαια ταχύτητα που μπορεί να αναπτύξει στο συγκεκριμένο σημείο της τροχιάς, η οποία καθορίζεται μόνο από την κλίση του δρόμου, εμφανίζεται ως πληροφορία στην εφαρμογή. Με βάση την ταχύτητα με την οποία κινείται ο μοτοσυκλετιστής και τη μάζα του οχήματος καθορίζεται η απαιτούμενη κεντρομόλος δύναμη η οποία αν υπολοίπεται σε σχέση με αυτή που προσδίδει στον μοτοσυκλετιστή η κλίση του οδοστρώματος οδηγεί σε εκτροπή από την κίνηση πάνω στην καμπύλη στο συγκεκριμένο σημείο και την κίνηση κατά την εφαπτομένη στο σημείο αυτό. Ο χρήστης έχει τη δυνατότητα να μετακινεί τη θέση του μοτοσυκλετιστή και να παρατηρεί με τον τρόπο αυτό την μεταβολή στην ακτίνα καμπυλότητας καθώς και τη μέγιστη στιγμιαία ταχύτητα που μπορεί να αναπτύξει ο μοτοσυκλετιστής με βάση την κλίση του οδοστρώματος.

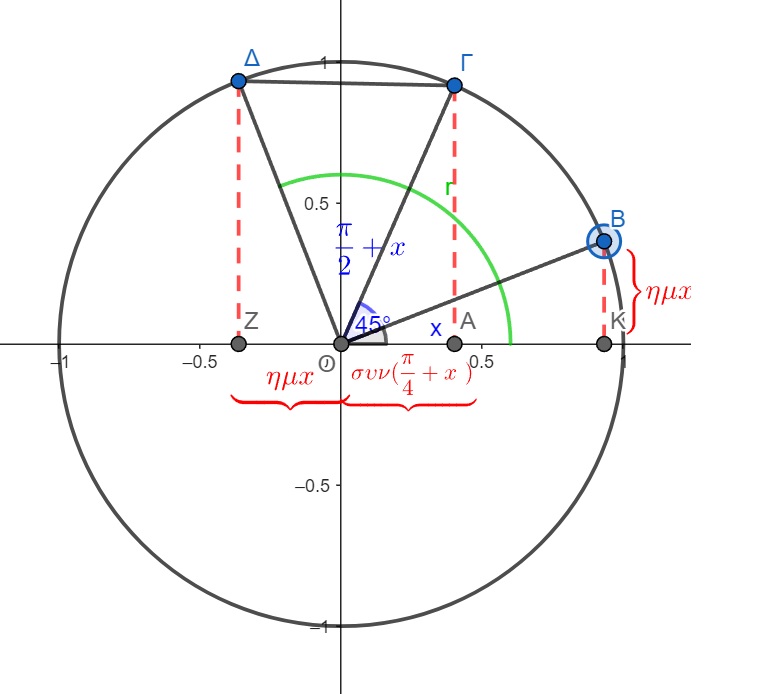
Επίλυση τριγωνομετρικής εξίσωσης που εμπλέκει συνημίτονο και ημίτονο με διαφορετικά ορίσματα

Στο παραπάνω link δίνεται εφαρμογή σε geogebra που σχετίζεται με την παρουσίαση “Επίλυση εξισώσεων με εναλλακτικούς τρόπους” https://ptsampouka.sites.sch.gr/index.html Η εφαρμογή υλοποιεί σχηματικά την επίλυση της τριγωνομετρικής εξίσωσης συν(θ+x)+ημx=α. Ο χρήστης μπορεί να πειραματιστεί μετακινώντας το σημείο Β που βρίσκεται πάνω στον τριγωνομετρικό κύκλο ώστε να επαληθεύσει την τιμή του x που προσδιόρισε θεωρητικά και αποτελεί τη λύση της εξίσωσης για τη μέγιστη τιμή του α που επιτρέπει την ύπαρξη λύσεων στην εξίσωση. Μπορεί επίσης να χρησιμοποιήσει την εφαρμογή ώστε πειραματικά να προσδιορίσει τις λύσεις της για τιμές του α μικρότερες από την επιτρεπτή.

Το παραπάνω link οδηγεί σε εφαρμογή που κατασκευάζει αριθμητικά με διάφορους βαθμούς προσέγγισης τη γραφική συνάρτηση της παράγουσας (αρχική συνάρτηση) για οποιαδήποτε συνεχή συνάρτηση δώσει ο χρήστης ακόμα και στην περίπτωση που δεν υπάρχει κλειστός τύπος της παράγουσας. Ο χρήστης έχει τη δυνατότητα να πειραματιστεί με την προσεγγιστική και οριακή διαδικασία στον προσδιορισμό της γραφικής παράστασης της παράγουσας μέσα από τη μετακίνηση 2 δρομέων παρέχοντας με αυτόν τον τρόπο νοηματοδότηση στην έννοια της παράγουσας.Η εφαρμογή συνοδεύεται επιπλέον από φύλλο εργασίας με ασκήσεις που αναφέρονται στην ταχύτητα και τη θέση ενός κινητού ώστε ο χρήστης να εξοικειωθεί με τα εργαλεία της εφαρμογής και να κατανοήσει το νόημα της παράγουσας.